The Step Mode

The first mode to apply a rule is called Step mode. Here, one selected rule will be applied exactly once to the current host graph. The match morphism in the Step mode may be defined by the user analogously to a rule morphism: From menu Transform, we choose menu item Match and define the match morphism elementwise by clicking on a graph object in the left-hand rule side first, and then clicking on a graph object in the host graph. Of course, the corresponding graph objects must be of the same type or in case of inheritance connected through a parent-child relation, there must be a consistent mapping of the attributes, and the mapping must be compatible with the source and target functions of edges. Another possibility to define a mapping is to choose the Map mode of the context menu Edit Mode and then click on the corresponding objects in the LHS and in the host graph. Of course, a mapping also can be deleted by choosing Unmap from the same menu. Defining the match completely ``by hand'' may be tedious work. Therefore, AGG allows to complete a partial match by choosing the Transform menu item NextCompletion after having defined an arbitrary partial morphism. The partial morphism will be completed to a total match automatically. If there are several choices for completion, one of them is chosen arbitrarily. Calling Next Completion again, another completion is computed, if possible. In this way, all possible completions are computed and shown one after the other in the editor using equal numbers for corresponding objects. After having defined the match, we choose item Step in menu Transform, and the rule will be applied to the host graph once at the given match. The result is shown in the graph editor. Thereafter, the host graph can immediately be edited, for instance to improve the layout of the new graph. Afterwards, any other rule may be selected and applied to the new graph in the Step mode as described above.

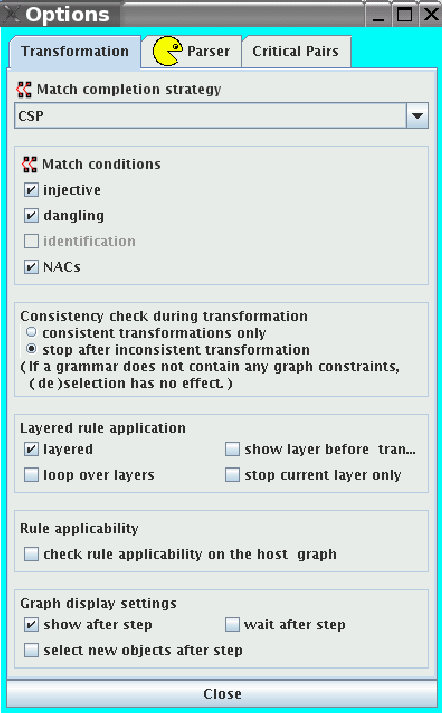
In AGG transformation options can be chosen by clicking item Options... of menu Preferences. The options are shown in Figure 21.

The first option defines a match completion strategy:

• CSP - Constraint Solving Problem,
• CSP w/o BJ - Constraint Solving Problem without Back Jumping,
• Simple BT - Simple Back Tracking.

More details described in the paper on efficient graph pattern matching by Michael Rudolf (http://tfs.cs.tu-berlin.de/agg/match.ps).

Figure 21: Transformation Options

For a very simple host graph (for example without attributes), the simple strategy Simple BT might be the fastest, whereas for our ShortestPath example we chose CSP which can be considered as standard strategy .
Options injective, dangling, identification and NACs define the properties of selected match completion strategy for direct transformation step.
Since AGG has a formal foundation based on the algebraic approach to graph transformation and the theoretical concepts are implemented as directly as possible AGG offers clear concepts and sound behavior concerning the graph transformation. Generally, to define a direct transformation step we have used the so-called single-pushout (SPO) approach to graph transformation in the category of graphs and partial graph morphisms. Switching on the gluing condition, combining the dangling and identification conditions, allows to realize the so-called double-pushout (DPO) approach in the category of graphs and total graph morphisms in the operational point of view.

Furtheron, two options allow to decide how graph consistency constraints influence the graph transformation process.

• Option consistent transformation only means that graph transformation steps with a consistent result graph will be performed only. The graph transformation process will not be stopped.
• Option stop after inconsistent transformation means that the graph transformation process will be stopped after the first transformation with an inconsistent result graph.

These options have an effect only, if the graph grammar contains graph consistency conditions.

Options for layered rule application have the following meaning:

• Option layered allows to use rule layers during graph transformations. Generally, rules given by a graph grammar are applied non-deterministically. A rule layer can be set for each rule or a set of rules. These layers fix the order how rules are applied. The interpretation process first has to apply rules of layer 0 as long as possible, then rules of layer 1, etc. That gives the possibility to specify a simple control flow on graph transformation.
• Option show layer before transform gives the possibility to change the layers before the graph transformation starts.
• Option loop over layers allows to continue graph transformation by beginning on the smallest layer again and continuing as long as possible.
• Option stop current layer only means that the graph transformation on the current layer will be stopped, if menu item Stop of menu Transformation is chosen. Thereafter, rules of the next layer will be applied, etc.

If option check rule applicability on the host graph is set, each rule will be checked whether it is applicable to the current host graph. This check will be done after each graph transformation step. Visually, the name of a non-applicable rule will be gray-colored in the grammar tree view. Alternatively, you can use menu item Check Rule Applicability of pop-up menu GraGra to perform this check only once. Using button Undo allows to switch off this check.

Further options define a kind of display settings of the graph transformation process.

• Option show after step causes that the altered host graph will be shown after each graph transformation step during the interpretation process. If this option is not set, the altered host graph will be shown at the end of the transformation process only.
• Option wait after step means that the transformation process will be paused after each succesful match and step to give the possibility to see the current match and a rule of the application. Entering any key allows to continue the transformation process.
• Option select new objects after step means that the new graph objects will be selected after each step to improve the visualization of the graph transformation process.

To get the previous state of the host graph after a transformation step or process has been done you can use menu item Undo of menu Transform. Alternatively, you can use menu item Reset Graph of pop-up menu GraGra.

Let us illustrate the transformation process by transforming the start graph of our ShortestPath example using the rules of graph grammar ShortestPath.ggx. We will go through a transformation session in Debug mode in order to show all important intermediate transformation steps.