Graph Parser

AGG provides a graph parser which is able to check, if a given graph belongs to a certain graph language determined by a graph grammar. In formal language theory, this problem is known as the membership problem. Here, the membership problem is lifted to graphs. This problem is undecidable for graph grammars in general, but for restricted classes of graph grammars it is more or less efficiently solvable.
Usually, a graph grammar is given to generate all graphs of a graph language. For parsing, all rules of the graph grammar have to be inverted. Applying the inverted rules in a right way, all graphs of the corresponding graph language can be reduced to the start graph of the grammar.
In AGG not all kinds of rules can be automatically inverted. That's why the graph parser expects already a so-called parse grammar containing reducing parsing rules and a stop graph. Given an arbitrary host graph, AGG tries to apply the parsing rules in a way that the host graph is reduced to the stop graph. If this is possible, the host graph belongs to the determined graph language and there is a derivation sequence from the host graph to the stop graph, otherwise the host graph does not belong to the graph language.

AGG offers three different variants of a parsing algorithm being based on backtracking. The parser builds up a derivation tree of possible reductions of the host graph. The leaves of this tree are either dead ends, i.e. leave graphs where no rule can be applied anymore but non-isomorphic to the stop graph or the stop graph. In this case, the parsing was successful. Since simple backt racking has exponential time complexity, the simple backtracking parser is accompanied by two further parser variants exploiting critical pair analysis for rules.

Critical pair analysis can be used to make parsing of graphs more efficient: decisions between conflicting rule applications are delayed as far as possible. This means that non-conflicting rules are applied first to reduce the graph as much as possible. Afterwards, the conflicting rules are applied, first in non-critical situations and when this is not possible, in critical ones. In general, this optimization reduces the derivation tree constructed, but does not change the worst case complexity.

The parsing process might not terminate, therefore layering conditions have to be defined to guarantee termination of the parsing process. Parsing of non-layered or layered graph grammars can optionally be based on critical pair analysis.

The graphical user interface of the graph parser allows to consider the parsing process step-by-step. The parser menu and options are described below.

The parser menu is available from the menu bar and contains the following items:

• Open - Opens a user dialog to initialize the parser and then changes to the parser GUI.
• Start - Starts the parsing process.
• Stop - Stops the parsing process.
• back - Returns to the main AGG GUI.

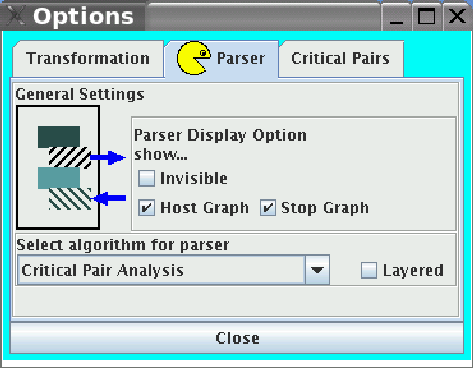
The options for the parser are available in menu Preferences / Options.... They are shown in Figure 62 and described below.

Figure 62: The parser options

• Parser Display Option is used to configure the visualization of a parsing process,
• Invisible can be used to make the host graph and/or the stop graph invisible,
• Host graph - the host graph is visible,
• Stop graph - the stop graph is visible,
• layered means layered parsing process: First all rules of one layer are applied as long as possible before the rules of the next layer are applied,
• Select algorithm for parser concerns the variant of parsing algorithm to be used. Dependent on the use of critical pairs the user may choose:
  • Critical Pair Analysis¹⁰ uses critical pair analysis to check if potentially conflicting rules really exclude rule applications in the actual host graph and applies non-conflicting rules first.
  • Semi-optimized backtracking¹¹ applies non-conflicting rules first.
  • Backtracking without optimization does not use critical pairs.

Before the parsing process can start, we have to set the needed data in the Starting Parser dialog shown in Figure 63. This dialog is invoked by item Open of menu Parser.

The items and buttons of the starting dialog are exlpained bellow:

• Select Host Graph waits for selecting or loading a grammar which contains a host graph.
• Select Stop Graph waits for selecting or loading a parsing grammar which contains the parsing rules and a stop graph.
• Select Critical Pairs has a special meaning. The critical pairs are connected with their parsing rules. Therefore, the parsing grammar has to be selected to generate critical pairs. If the critical pairs are already generated and stored, they can be loaded.
• The Next button moves the selector to the next item. If the initialization is completed, the Finish button appears.
• The Finish button closes the user dialog and opens the parser GUI.
• The Cancel button cancels the user dialog.

Figure 63: The starting parser dialog

Figure 64 shows the Parser GUI for example ''Statecharts''.

Figure 64: The parser GUI

Using menu item Parser / Start start the parsing process.

Graph parsing in the context of visual language parsing is described in:

• ''Application of Graph Transformation to Visual Languages'' by R. Bardohl, M. Minas, A. Schürr and G. Taentzer (http://www.cs.tu-berlin.de/gabi/gBMST98.ps.gz).
• ''Efficient Parsing of Visual Languages based on Critical Pair Analysis and contextual Layered Graph Transformation'' by P. Bottoni, A. Schürr and G. Taentzer (http://www.cs.tu-berlin.de/agg/parser/BST-long.ps).

More about the facilities of the parser and the critical pair analysis in AGGis described in the diploma thesis of Thorsten Schultzke (in German): ''Entwicklung und Implementierung eines Parsers für visuelle Sprachen basierend auf kritischer Paaranalyse'' (http://tfs.cs.tu-berlin.de/agg/Diplomarbeiten/ThorstenDiplomarbeit.ps).