Consistency checking in   

 

Consistency of Conditional Graph Grammars

AGG 1.2.0 supports a consistency control mechanism which is able to check if a given graph satisfies certain consistency conditions specified for a graph grammar.  Consistency conditions describe basic properties of graphs as e.g. the existence of certain elements, independent of a particular rule. We propose a transformation of global consistency conditions into post application conditions for individual rules. A so-constructed rule is applicable to a consistent graph if and only if the derived graph is consistent, too. A graph grammar is consistent if the start graph satisfies the consistency conditions and the rules preserve this property. In AGG, consistency conditions are defined on the basis of graphical consistency constraints.  A graphical consistency constraint is a total injective morphism c : P -> C ,  the left graph  P  called premise and the right graph  C   conclusion.  A graphical consistency constraint is satisfied by a graph G,  if for all total injective morphisms  p : P -> G  there is a total injective morphisms  q : C -> G  such that  q o c = p .  If  CC  is a set of  graphical consistency constraints,  we say that  G  satisfies  CC ,  if  G  satisfies all constraints in  CC. .  The post application conditions generated from graphical consistency constraints ensure consistency of a graph grammar during rule application.

Note: If you use attributed graph grammar please do not forget to set all attribute members of the graph objects in all atomic consistency constraints :     - use variables or constants in the left-hand side of a constraint     - use variables or constants ( no expressions ) in the right-hand side of a constraint     - you can use attribute conditions to define relations between variables The translation of consistency constraints into post conditions might cause problems for rules with attribute conditions.

 

Graphical user interfaces

In the following, we consider menus to create graphical constraints, formulas or post application conditions and to check consistency of a graph grammar.

To create an atomic graphical constraint use :  menu item  New Atomic Constraint  of File menu menu item  New Atomic Constraint  of GraGra popupmenu

An atomic constraint can contain more as one conclusions. Default size of conclusions is 1. To create more conclusions use menu item  New Conclusion  of Atomic Constraint popupmenu.  The left , right graphs and morphism of an atomic constraint will be edited like a rule. Atomic Constraint popupmenu.

To create a constraint (formula) use :  menu item  New Constraint  of File menu menu item  New Constraint  of GraGra popupmenu

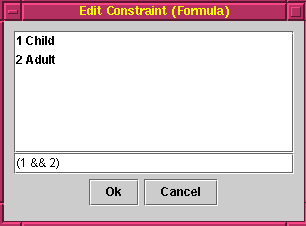
We can define a boolean formula using atomic consistency constraints as variables. To edit a formula use menu item  Edit  of Constraint popupmenu. You get a formula editor. Constraint (formula) popupmenu. The formula editor shown here contains atomic constraints in ''Carrousel`` example shown below. Formula editor

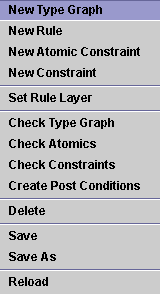
File menu and GraGra popupmenu are shown here.      File menu and GraGra popupmenu

To generate post application conditions from all atomic constraints for all rules at the same time use menu item   Create Post Conditions   from menu Analyzer / Consistency Check from all atomic constraints for an espesial rule  use menu item   Create Post Conditions   from Rule popupmenu  from an espesial atomic constraint for all rules  use menu item   Create Post Conditions   from Atomic Constraint popupmenu  from an espesial atomic constraint for an espesial rule - NOT JET IMPLEMENTED

To check consistency of a graph grammar use : menu item  Check Atomics  of Analyzer / Consistency Check menu or GraGra popupmenu  menu item  Check Constraints  of Analyzer / Consistency Check menu or GraGra popupmenu  menu item  Check Graph  of Atomic Constraint popupmenu or Constraint popupmenu Consistency Check menu.

 

Sample Consistency Checking in AGG

Let us consider graph grammar "MerryGoRound" as an example for consistency checking. The grammar is stored in   "carrousel.ggx" . The carrousel is modeled by a node  of type 'carrousel` . Each boat modeled by a node  of type 'boat`  is connected by a blue edge to the carrousel node. People on the carrousel are modeled by nodes  of types 'child`  and  'adult` , connected by black edges to the boat they are sitting in. We use flags 'stop' and 'go' modeled by a red rectangle node and black rectangle node respectively. The flags are connected by blue edges to the carrousel node. Additionally, we have two consistency conditions. The first condition ensures that whenever there is a child in a boat of the carrousel, there is an adult in this boat, too. The second condition ensures that whenever there is an adult in a boat ,there is a child in this boat, too. In this case the carrousel may start to move, i.e. the 'stop' flag on top may be replaced by a 'go' flag.

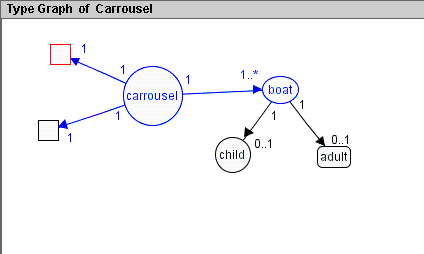
The type graph of the grammar is shown in Figure 1. Figure 1. The carrousel type graph.

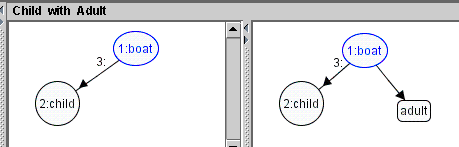
The consistency constraints: Child and Adult The first atomic consistency constraint Child is shown in Figure 2. Figure 2. Atomic consistency constraint  Child The second atomic consistency constraint Adult is shown in Figure 3. Figure 3. Atomic consistency constraint  Adult

Additionally, we can define a boolean formula using the atomic consistency constraints just defined as variables.  The formula will be defined in editor shown in Figure 4. Figure 4. Formula editor

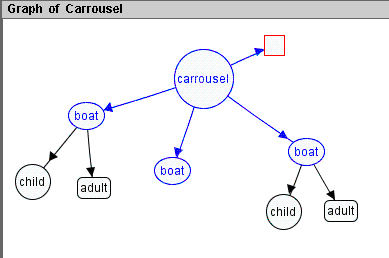
The start graph of the grammar is shown in Figure 5. Figure 5. The carrousel graph.

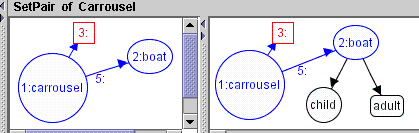
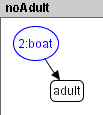
Now the Rules: SetPair, SetChild, SetAdult, Go, Stop, Empty The first rule SetPair with tree NACs ensures that only a pair of one child and one adult can enter an empty boat.  The rule is shown in Figure 6. Figure 6. Rule SetPair The NACs of  rule SetPair are shown in Figure 7. Figure 7. NACs of rule SetPair

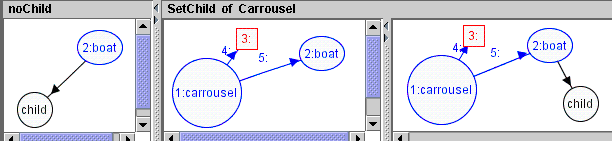
The rule SetChild with a NAC ensures that a child can only enter a boat without another child. Figure 8. Rule  SetChild We generate two post application conditions  fromChild  and  fromAdult  from consistency constraints  Child  and  Adult to ensure that a child can only enter a boat with an adult.  Post application conditions of the rule   SetChild

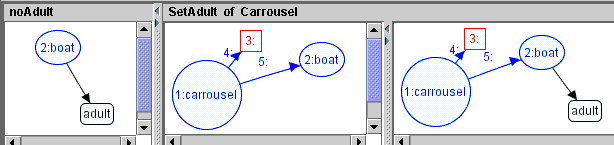
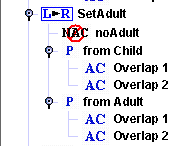
The rule SetAdult with a NAC ensures that an adult can only enter a boat without another adult. Figure 9. Rule SetAdult We also generate two post application conditions from consistency constraints to ensure that an adult can only enter a boat with a child.  Post application conditions of the rule   SetAdult

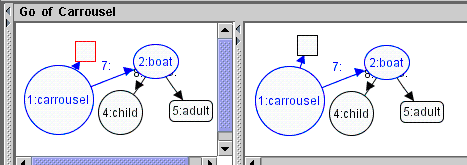
The rule Go can be applied if and only if each boat contains a child and an adult or is empty.  This is ensured through post application conditions generated from consistency constraints.  An example of an atomic post application condition is shown in Figure 10a. Rule Go is shown in Figure 10. Figure 10. Rule Go

Now an example of a post application condition of the rule Go. An atomic of the post application condition fromChild is shown in Figure 10a. Figure 10a. Overlap 1 : An atomic of the post application condition fromChild

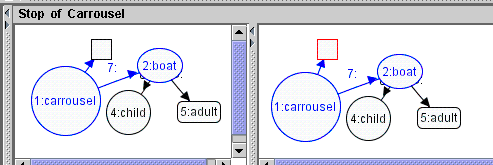
The rule Stop is shown in Figure 11. Figure 11. Rule Stop

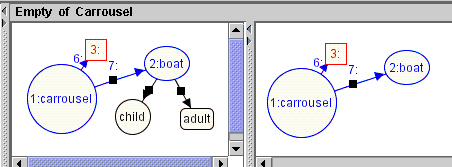
The rule Empty is shown in Figure 12. Figure 12. Rule  Empty

 

Consistency of conditional graph grammars is described in:

Ensuring Consistency of Conditional Graph Grammars - A Constructive Approach -  by Reiko Heckel and Annika Wagner, 1995 .

Modellierung und Nachweis der Konsistenz von verteilten Transaktionsmodellen für Datenbanksysteme mit algebraischen Graphgrammatiken  by Manuel Koch (in German).  Bericht-Nr. 96-36.  Forschungsberichte des Fachbereichs Informatik an der Technischen Universität Berlin.

Konzeption und Implementierung eines Verfahrens zum Nachweis der Konsistenz in einer attributierten Graphgrammatik  Diploma thesis of Michael Matz (in German)

 

Revision: